Poker math can be confusing at times. One of the biggest head-scratchers is around the concept of breakeven, or 0EV, and how that really works. Since we either win the hand (making money), or lose the hand (losing money), and pretty much never walk away with exactly $0. So today we’re going to explain how a bluff can end up being breakeven, using some simple poker math.
We’re going to answer this through the lens of a question sent in by Jane. This is a basic math question, but one that you need to fully understand. Grasping this concept will help you catch on to some of the more difficult things we talk about in other poker videos. Jane’s question is this:
“If I bet half pot on a river bluff and villain folds 33% of hands, I win the pot. Why is that ‘break even’ or 0EV?”
Before we start let me just say that this question is pretty common and is completely OK to ask. Poker math can seem a little confusing at first, but once you get it, you will improve on and off the felt. Now I can see how it is confusing when we have 0EV but we are winning at least some of the time. How can you possibly have 0EV but win?
Well, let’s look at the break-even percentage formula and the basic EV formula. We would use the advanced EV formula if we would ever consider bet/3betting, or if we suspected we were ever ahead when getting called. But since we are pure bluffing, let’s assume that if villain ever continues that we lose and concede and plug these numbers into our poker software sheet.
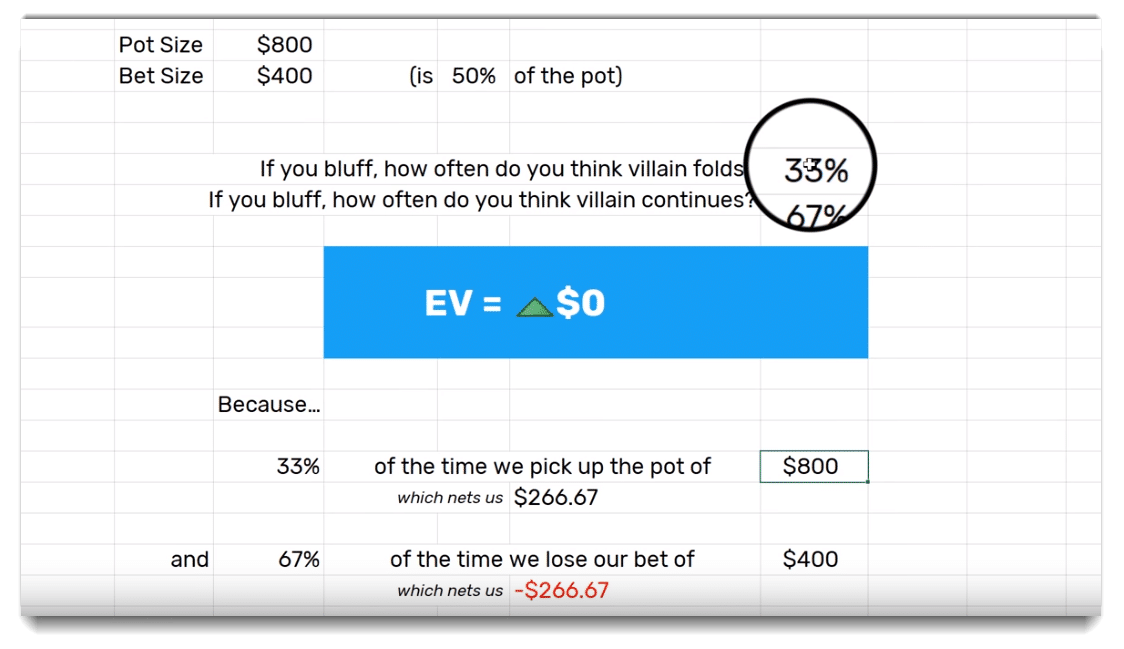
So we are looking at excel and we decided that the pot was $800 and the best size was $400. Well, we seem to think our opponent is folding ⅓ of the time and when we plug this in using the break-even percentage formula:
BE% = Risk/(Risk+Reward)
And given these inputs, our EV is at $0.
This is because of the EV formula, which is:
EV = (Win% * $Win) – (Lose% * $Lost)
In this situation, 33% of the time we are thinking we are going to pick up the pot uncontested. Meaning 33% of the time, we pick up that $800, netting us a total of +$266.67. And then when we bluff and our opponent doesn’t fold, we will lose 67% of the time. Well when we lose, we are losing our $400 bet. Furthermore, we are losing $400, ⅔ of the time, netting us -$266.67. When we add both of those numbers like the EV formula informs, you see an overall EV of $0.
Did you know that this kind of work is the foundation of GTO concepts like value & bluff combos within a betting range? Click here for the beginner’s guide to GTO poker.
But do note that if you change the size of your bet in context of the pot and/or the rate at which your opponent folds, your EV can change pretty quickly. For example, if our opponent folds 45% of the time instead of 33%, we suddenly go positive and if they fold 10% of the time we go very negative. And of course, this math is consistent whether you are studying live tournament hands or reviewing online poker site hands.
So things to take away from this is memorizing the formulas, understanding the basic principals and just working through these sort problems until you get a grasp on the concept. Once you understand how poker math works, you will become a much better player and will be more confident in your ability to discern when to play and when to fold.
If you are looking to take the next step when it comes to poker math, I fully suggest picking up Poker Math That Matters – the best book for getting the poker math down quickly. You can pick up your copy with an instant-download here: Buy Poker Math That Matters. Enjoy!
